Etymology

Middle English: from Old French constraindre, from Latin constringere ‘bind tightly together’.

Reflectio: Constraint types

What types of constraints do You take into account when You:

make a decision D

when You solve a problem P

???

Constraint types

logic / contingency

space

time

energy

computational complexity

human resources

material resources

eco(log|nom)ical constraints

socio-political

psycho-cognitive

legal

moral

Constraint programming

%22Illustration%20on%20a%20black%20background%20depicting%20the%20concept%20of%20'constraint%20programming'.%20A%20set%20of%20interconnected%20nodes%2C%20each%20labeled%20as%20a%20variable%2C%20with%20chains%20or%20links%20representing%20constraints.%20Some%20nodes%20glow%20to%20indicate%20they%20are%20satisfying%20their%20constraints%2C%20while%20others%20are%20dim%20to%20show%20they%20aren't.%22

"Illustration on a black background depicting the concept of 'constraint programming'. A set of interconnected nodes, each labeled as a variable, with chains or links representing constraints. Some nodes glow to indicate they are satisfying their constraints, while others are dim to show they aren't."

Constraint programming is a programming paradigm where relationships between variables are expressed as constraints. The objective is to find values for these variables that satisfy all given constraints. It is particularly useful for solving combinatorial problems, such as scheduling, planning, and resource allocation, where traditional algorithms might be inefficient. Instead of specifying steps to achieve a solution, one defines the desired properties of a solution, and the system determines a valid assignment, if one exists.

Constraint Satisfaction Problem

A Constraint Satisfaction Problem (CSP) is a mathematical problem defined by a set of variables, a domain of possible values for each variable, and a collection of constraints specifying permissible combinations of values. The goal is to assign values to the variables such that all constraints are satisfied. Common examples include the Sudoku puzzle, where each cell is a variable, digits 1-9 are the domain, and the rules of Sudoku are the constraints. Other examples:

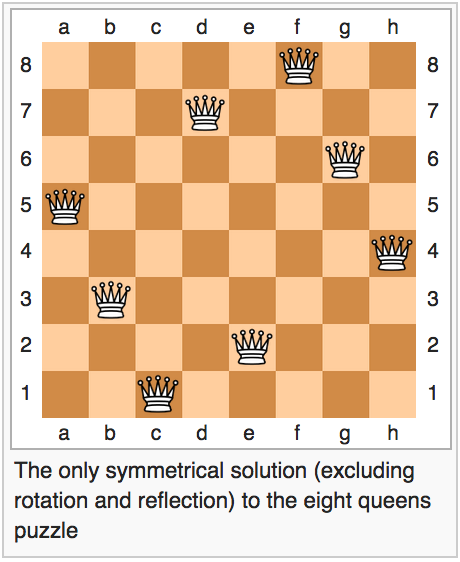
eight queen problems

map coloring problem

Exercise: Adam and Eve scheduling

Adam and Eve are happily married and have two cute sons, Cain and Abel. In general they love each other, but sometimes divirgent opinions relating to house management lead to unnecessary conflicts. To reduce such conflicts, Adam proposes to optimize, starting with following facts: there are four rooms (kitchen, bath, living room, sleeping room) in their house and they want to have each room in an absolutely clean state at least once in a week. Cleaning of sleeping room and bathroom necessitate investment of 2 hours each, cleaning of living room and kitchen costs 3 hours each. In order to keep family healthy & restauration costs low, a hot meal is cooked at least 4 times in a week and children also demand one cake a week. Cooking takes 1 hour, baking 2 hours. After cooking or baking, kitchen becomes dirty and Eve demands that kitchen is clean on Sunday evening. Adam has one hour time on Monday and Wednesday, three hours time on Thursday and fours hours time on each weekend day, Eve has two hours on Tuesday, three hours on Friday and four hours on each weekend day. Ideally, they would like to maximize the amount of time they invest into cleaning & cooking.

Optional: Act of bringing little Cain & Abel to a playground for two hours results in less entropy at home and thus reduces living room cleaning cost to two.

Assignment

Everyone: define tasks (and their lengths), resources (and their availability), precedence relations (if any), capacity constraints (if any) and costs of optional tasks (if any)

IOPS group: find the optimal solution using some constraint programming library (GPT4 can show You how to use it)

Solution

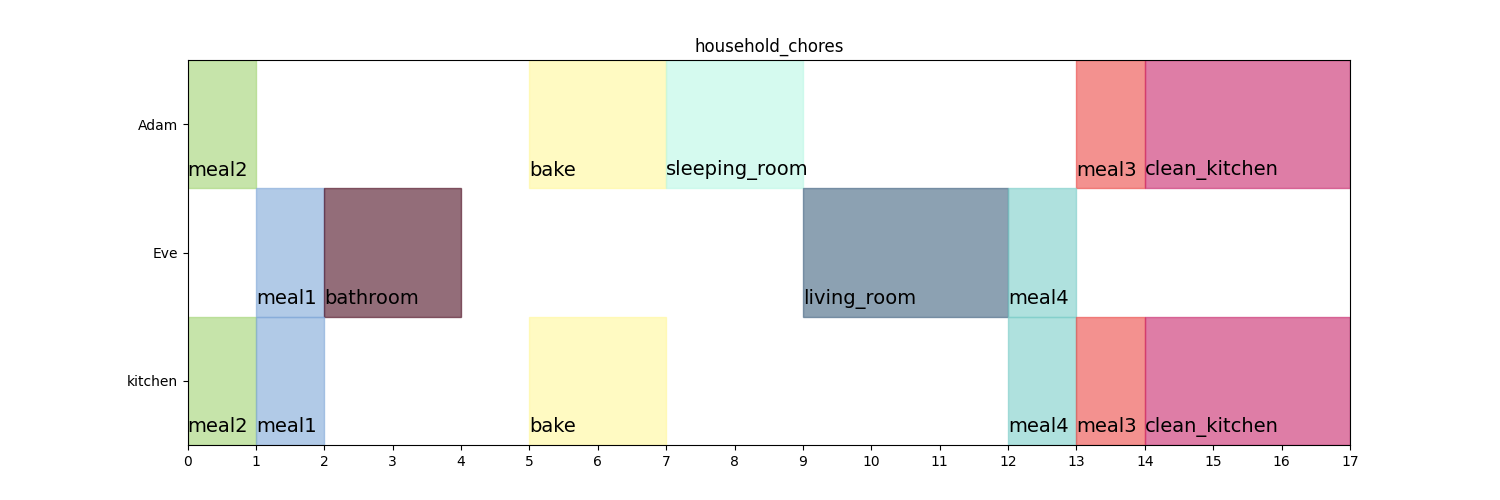
#Adam has one hour time on Monday and Wednesday, three hours time on Thursday and fours hours time on each weekend day, Eve has two hours on Tuesday, three hours on Friday and four hours on each weekend day.  Define pyschedule resources with correctly defined periods and horizons.

#Monday: Adam x 1
#Tuesday:  Eva x 2
#Wednesday: Adam x 1
#Thursday: Adam x 4
#Friday: Eva x 3
#Saturday: Both x 4
#Sunday : Both x 4

from pyschedule import Scenario, solvers, plotters, alt

# Define the scenario
S = Scenario('household_chores', horizon=15)  # Two weeks

# Define the resources, resource costs are not obligatory but it's more fun with them
adam = S.Resource('Adam',periods=[0,3,4,5,6,7,11,12,13,14])
eve = S.Resource('Eve',periods=[1,2,8,9,10,11,12,13,14])

kitchen=S.Resource('kitchen')

# Define the tasks and their durations
task_costs = {
    "meal1": {"length":1,"delay_cost":1},                # 1 hour, schedule towards beginning of the week
    "meal2": {"length":1,"delay_cost":1},             
    "meal3": {"length":1,"delay_cost":-1},               
    "meal4": {"length":1,"delay_cost":-1},               # 1 hour, schedule towards end of the week
    "bake": {"length":2,"delay_cost":0},                  # 2 hours (1 cake)
    "sleeping_room": {"length":2,"delay_cost":0},  # it seems there is a bug for tasks longer >1 
    #"CSR1": {"length":1,"delay_cost":0},          # one way how to address the bug is to split long tasks into sub-tasks coupled by tight preference constraints
    #"CSR2": {"length":1,"delay_cost":0},          # 
    "bathroom": {"length":2,"delay_cost":0},       # 2 hours
    "living_room": {"length":3,"delay_cost":0},    # 3 hours
    "clean_kitchen": {"length":3,"delay_cost":0}   # 3 hours
}

tasks={}
# Define alternative resources for each task
for task,costs in task_costs.items():
    print(task,costs)
    tasks[task] = S.Task(task,length=costs['length'],delay_cost=costs["delay_cost"])      #create new task
    tasks[task] += adam | eve               #assign resources to newly created task

#additional task-resource attributions
tasks["clean_kitchen"]+=kitchen
tasks["meal1"]+=kitchen
tasks["meal2"]+=kitchen
tasks["meal3"]+=kitchen
tasks["meal4"]+=kitchen
tasks["bake"]+=kitchen

#tight precedence constraints
#S += tasks['CSR1'] <= tasks['CSR2']

#optional tasks
#tasks['playground'] = S.Task('playground',length=2,schedule_cost=-1)
#tasks['playground'] += alt(adam,eve)

#additional constraints
S += tasks['meal1'] < tasks['clean_kitchen'] 
S += tasks['meal2'] < tasks['clean_kitchen'] 
S += tasks['meal3'] < tasks['clean_kitchen'] 
S += tasks['meal4'] < tasks['clean_kitchen'] 
S += tasks['bake'] < tasks['clean_kitchen'] 

# Solve the scenario
solvers.mip.solve(S,msg=1,kind='GUROBI')

print(S)
print(S.solution())
print(adam.periods)
# Plot the schedule
plotters.matplotlib.plot(S)

Python libraries

pyschedule example

https://github.com/python-constraint/python-constraint

https://github.com/timnon/pyschedule

Note: install the most recent fork, (e.g. pip3.10 install "pyschedule"@git+"https://github.com/ppoile/pyschedule/#subdirectory=src")

Linear Programming

Linear Programming (LP) is a mathematical method used to find the best outcome in a model whose requirements are represented by linear relationships. It's like playing a game where you need to achieve the highest score (maximize) or the lowest score (minimize) under certain rules. These rules are your constraints, like how much money you can spend or how many hours you have. The score you're trying to optimize is called the objective function, and it's also a linear equation. LP helps you figure out the best way to play this game, balancing all the rules, to achieve your goal, whether it's making the most profit, using the least resources, or something similar. It's a powerful tool for decision-making in business, engineering, economics, and more.

Simplex Algorithm

Imagine you have a map with various paths and you need to find the shortest way to a treasure. Each path has its own rules, like how much weight you can carry or how fast you can travel. The Simplex algorithm helps you navigate these paths and rules to find the most efficient route to the treasure.

In technical terms, it deals with equations representing constraints (like the rules of each path) and a goal (like reaching the treasure in the shortest time). The algorithm iteratively explores vertices on a multidimensional shape (the map), checking at each step if it's closer to the best solution. It's like checking each intersection on a map to see if you're closer to the treasure. This continues until it finds the most efficient route, giving you the best solution to your problem.

Fossil-Free Frontier

This project’s main goal is a linear programming model that re-envisions ambitious yet feasible renewable energy goals for key regions by focusing on the trade-offs between different fossil-free energy sources. For this, the project focuses on the data of four common fossil-free energy sources: wind, solar, nuclear and hydro, as well as relevant variables such as Cost, Reliability, Existing Energy Mix and Public Approval.

Summary

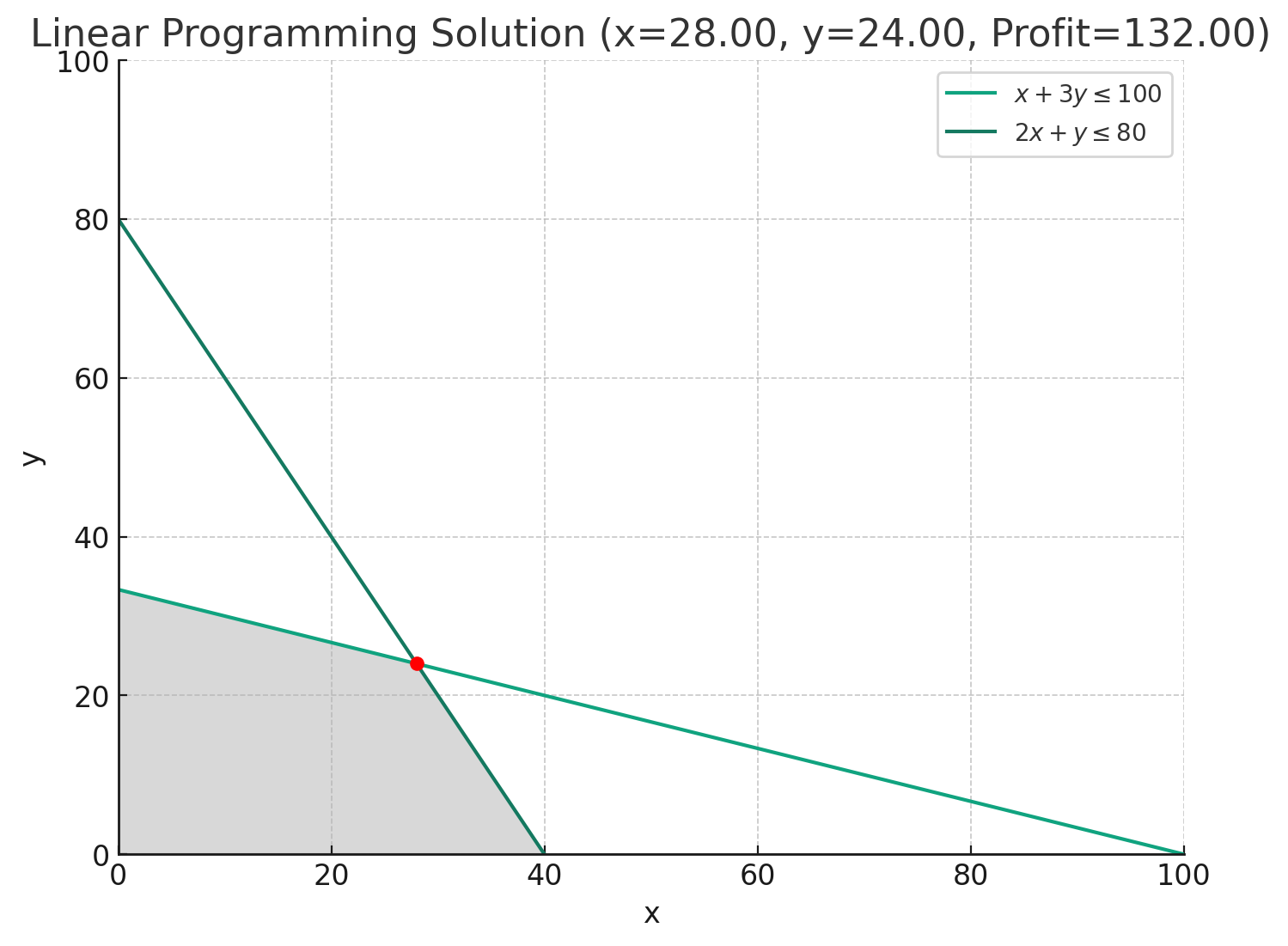
Focus: LP deals specifically with linear equations and inequalities. This means it works with problems where relationships are represented as straight lines (hence 'linear').

Objective: It always aims to find the maximum or minimum value of a linear equation, known as the objective function. For example, maximizing profit or minimizing cost.

Method: LP uses specific mathematical methods, like the Simplex algorithm, to find the best solution.

Constraints: All constraints in LP are linear (straight-line relationships). For instance, you can't spend more than a certain budget, or you need at least a certain amount of some ingredient.

Solutions: Solutions in LP are often numerical and can include fractions or decimals.

Diet Problem

Diet Problem (DP) involves finding the most cost-effective diet that meets all nutritional requirements. Imagine you have a list of foods, each with its own nutritional content and cost. Your goal is to choose a combination of these foods that provides all the necessary nutrients (like vitamins, proteins, carbohydrates, etc.) for the least possible cost. You set up equations for each nutrient, ensuring your diet doesn't fall short or exceed what's needed. Then, you use linear programming to minimize the total cost while satisfying these nutritional constraints. It's like solving a puzzle where you balance your health needs against your budget, finding the best possible dietary plan.

Tangle v0.0.1 Optimization

Here is a CSV containing information about nutritive values of different vegetables growable in a German garden, last column also contains expected yield per square meter. Please provide a combination of vegetables which would satisfy nutritive need of an adult man so that the surface on which the vegetables grow is minimized. To have the meal diversified, there should be not more than 300g of certain vegetable.

Constraint Programming Summary

Focus: CP is more general and can handle a wide variety of constraints, not just linear ones. It can deal with logical conditions, like "either-or" situations, and can include non-linear relationships.

Objective: CP doesn't necessarily have an objective function to optimize. Instead, it focuses on finding solutions that satisfy all the given constraints.

Method: It uses different algorithms than LP, often based on search techniques, like backtracking or heuristics.

Constraints: Constraints in CP can be diverse - linear, non-linear, logical conditions, etc. For example, a constraint could be that a certain task must be done before another can start.

Solutions: Solutions in CP are often discrete (like whole numbers) and can involve deciding between different options or scenarios.